Introduction :
Création d’une approche d’exécution contrôlée par la méthodologie mathématique de calcul de position suivante.
Méthodologie et approche proposée:
Architectures et fonctionnalités:
Le principe de cette étude est de créer une méthode topographique et géodésique simple et économique qui permet de représenter graphiquement les terrains peu profonds avec des fonds meubles constituées pour des apports de ruissellement et des vases.
Parmis les conditions de la méthodologie, on traite la méthode de calcul de la position d’un point (dans le cas du bateau).
Le calcul de la position du bateau pose le problème mathématique et la lame d eau de la retenue commence du 0 en profondeur au niveau de la berge et allant à la profondeur maximale au niveau du lit de l’oued.
1 ère condition d’exécution:
Barque à fond plat équipe d’un échosondeur et récepteur-émetteur GPS et réflecteur. On a opté pour l’utilisation d’un zodiac motorisé dont on a installé l’équipement.
2ème condition:
Une station totale pour l’exécution d’une polygonation parallèle aux isobathes sur la rive.
3ème condition:
Un appareillage de transmissions des coordonnées et des profondeurs mesuré par échosondage.
4ème condition:
Un instrument de levé de détails selon les isobathes.
5ème condition:
Constitution dune brigade de 5 topographes. Pour le pilotage du bateau, le mesureur d’échosondage, le porte réflecteur croquiseur et transmetteur, l’operateur de la station et le topographe aliénateur.
La méthode mathématique
Calcul de la position du bateau : un problème mathématique
Le problème évoque dans le texte se résume à une situation géométrique simple : connaissance des distances r1, r 2 et r3 entre un point P(X, Y) et trois points donnes P1(x1, y1), P2(x2, y2) et P3(x3, y3) dans le plan, peut-on calculer la position du point P?
La manière la plus simple de résoudre ce problème est graphique. Le point P étant situe à la distance r1 du point P1, il doit se trouver sur le cercle de centre P1et de rayon r1.De manière analogue P doit aussi se trouver sur le cercle de centre P2 et de rayon r2, ainsi que sur le cercle de centre P3 et de rayon r3. Le point d'intersection des trois cercles fournit le point P (Fig. 1).
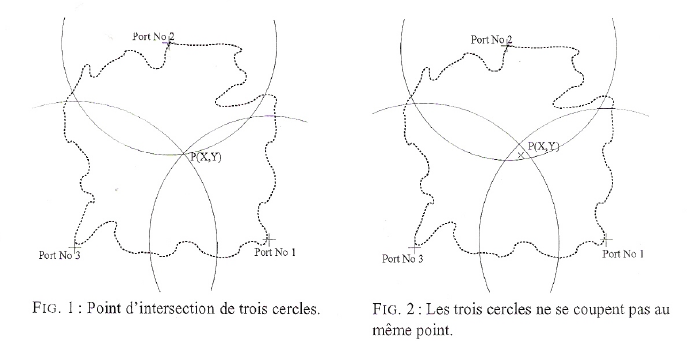
Malheureusement, cette construction n'est possible que si les distances, c'est- à-dire les rayons des cercles sont mesurés de manière absolument exacte.
Dans le problème évoqué ci-dessus, les trois distances sont calculées à partir des temps de parcours du son des canons. Il faut donc prendre en compte des erreurs dans les mesures de ces temps de parcours.
De plus, il faut admettre que l'horloge du bateau, étant souvent secouée, n'est pas exactement synchronisée avec les trois horloges des ports. Dans ces conditions, les trois cercles ne se coupent pas en un point unique.
Le point P ne peut donc pas être déterminer de manière exacte, mais on «devine» qu'il doit se trouver quelque part dans la région où les trois cercles sont très proches l'un de l'autre (Fig. 2).
Nous allons maintenant d’écrire une méthode mathématique qui permet de résoudre ce problème. Commençons par définir quelques grandeurs significatives:
vs : vitesse moyenne du son dans l'air (0.340 km/s) ;
t1 : temps de parcours du son du 1er canon entre le port et le bateau, selon les calculs effectues sur le bateau (126 secondes) ;
t2 ; temps de parcours du son du 2ème canon (157 secondes) ;
t3 ; temps de parcours du son du 3ème canon (173 secondes) ;
T: erreur de synchronisation de l'horloge du bateau par rapport aux horloges terrestres.
Au moyen de ces notations, la distance r1 entre le bateau et le port No 1 peut s'exprimer de la distance correspondante a la distance euclidienne entre P(X, Y) et P1(x1, y1) ;
r1 =  (1)
(1)
D'autre part, on sait que la distance r1r1a été parcourue par le son du canon No 1. Ce son s'est propagé dans l'air à la vitesse vs durant le temps t1+ T (temps calculé + erreur de synchronisation). On peut donc exprimer r1 sous la forme
r1 =vs. (t1+ T) (2)
En soustrayant (1) et (2), on obtient l'équation
 = 0 (3)
= 0 (3)
Si l'on introduit la fonction ƒ1 (X, Y, T) =  (t1+ T) on peut se convaincre que les coordonnées (X, Y) de la position exacte du bateau et l'erreur d'horloge T font partie de l'ensemble des solutions de l'´equation
(t1+ T) on peut se convaincre que les coordonnées (X, Y) de la position exacte du bateau et l'erreur d'horloge T font partie de l'ensemble des solutions de l'´equation
ƒ1 (X, Y, Z) = 0 (4)
Opérant de manière analogue avec les deux autres ports No 2 et No 3, on peut conclure que les trois nombres cherchés X, Y et T doivent aussi faire partie de l'ensemble des solutions des équations ƒ2 (X, Y, Z) = 0 et ƒ3 (X, Y, Z) =0, avec
ƒ2 (X, Y, Z) =  (t2+ T)
(t2+ T)
ƒ3 (X, Y, Z) =  (t3+ T)
(t3+ T)
Ainsi posé, le problème consiste à résoudre un système de trois équations non linéaires à trois inconnues, qui peut être formulé sous la forme vectorielle
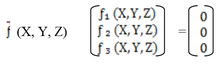
La résolution de cette équation s'effectue par linéarisation. Nous ne donnerons pas ici le détail des calculs, mais uniquement l'idée de la méthode de résolution. Rappelons que le point P(X, Y) obtenu après résolution de ce système n'est pas forcément un point appartenant simultanément aux trois cercles, mais un point optimal «le plus proche possible» des trois cercles.
Supposons que X0, Y0 et TO soient des valeurs approximatives de la solution cherchée X, Y et T. De telles valeurs approchées peuvent être facilement devinées. Si ΔX=X-X0, Y =Y-Y0
et ΔT = T-T0 représentent les différences entre ces valeurs initiales approximatives et les valeurs cherchées X ,Y ,T et si l'on groupe ces différences dans un vecteur, 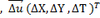 l'équation (5) se linéairessous la forme:
l'équation (5) se linéairessous la forme:
 (X0, Y0, T0)
(X0, Y0, T0)
 =
= (6)
(6)
Dans l'équation (6), J est la matrice jacobéenne de évaluée pour les valeurs initiales X0, Y0 et T0 c'est-à-dire:
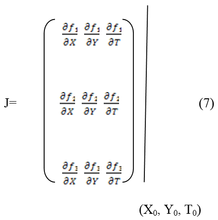
Le terme 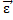 qui apparait dans l'équation (6) représente l'erreur de linéarisation au 2éme ordre. Celle-ci sera négligée dans la suite.
qui apparait dans l'équation (6) représente l'erreur de linéarisation au 2éme ordre. Celle-ci sera négligée dans la suite.
La résolution de l'équation vectorielle (6) fournit le vecteur 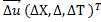 qui permet ensuite de calculer une nouvelle approximation X1 = X0 + ΔX , Y1 = Y0 + ΔY et T1 = T0 + ΔT de la solution, celle-ci étant de meilleure précision que l'approximation précédente.
qui permet ensuite de calculer une nouvelle approximation X1 = X0 + ΔX , Y1 = Y0 + ΔY et T1 = T0 + ΔT de la solution, celle-ci étant de meilleure précision que l'approximation précédente.
Pour calculer le vecteur  à partir de l'équation (6), il faudrait en principe résoudre le système d'équations linéaire
à partir de l'équation (6), il faudrait en principe résoudre le système d'équations linéaire
J. = −
= − (X0, Y0, T0). (8)
(X0, Y0, T0). (8)
L'équation (8) représente un système de trois équations linéaires à trois inconnues facile à résoudre.
Il est toutefois avantageux de pré-multiplier l'équation (8) par la matrice transposée JT et de r´résoudre ensuite le système
JT. J. = - JT
= - JT . (9)
. (9)
L'une des raisons de cette modification est la suivante : supposons qu'il y ait autour du lac un quatrième canon placé dans un quatrième port. Il est facile de deviner que la connaissance de la distance entre ce quatrième point fixe et le bateau permettrait au capitaine de déterminer sa position avec une meilleure précision.
Mathématiquement, cette modification conduirait à ajouter une quatrième équation au système (5), qui posséderait alors 4 équations mais seulement 3 inconnues (système surdimensionné)!
Il en serait de même pour le système d'équations linéaires (8). Un tel système ne peut pas être résolu comme un système linéaire «normal», mais il peut être résolu sous la forme transformée de l'équation (9).
Finalement, c'est en exécutant quelques itérations du même processus en prenant X1, Y1 et T1 comme nouvelles valeurs initiales que l'on améliore de proche en proche la précision de la solution. On obtient de cette façon les deux coordonnées X et Y du bateau, ainsi que l'erreur T de synchronisation de l'horloge du bateau par rapport aux horloges terrestres.
Cette méthode de calcul de positionnement est utilisée dans la méthode topographique de détermination de position dite trilateration.
Le récepteur GPS de la barque capte les signaux satellitaires et calcule la position des points.
Contrôlé par le mode de triangulation à l’aide d’une polygonation gérée par la station totale.
L’étude du cas concret présente le cas suivant:
Bibliographie et Référence
- Hervé Foch, Production of maps (16 /06/ 2010) (Infoterra France SAS)
- Michel Cances ,Etude de Spot et des Images, (2011 Toulouse)
- Ghannem et Drozdov, Astrogravimetria Mesurage et Compensation Moscou, (2007, Moscou)
- Suslin, triangulation et rattachement (2004 Moscou ( MGU))
- Bogomolov et Ghannem (MGU) Moscou Geodesie Spatiale Reseau et Rattachement
- Vida Maliene Liverpool John Moores Univesity Cartography
- Kasim Pinar Mersin Turkey (Cadastral mapping)
- Stojanka Brankovic, PROCEDURE OF LAND CONSOLIDATON SUPERVISION (Republic Geodetic Authority Belgrade, 24/06/2011 Serbie)
- Branko S.Bozic Serbie (Catography)
- Goloubev (MGU) Moscou.Reseau et mode de calcul
- Ghannem Ali ( Université El Manar Tunisie ) Methode bathymetrique
- Rosemberg (Université de Hanover Allemagne) Lecture de Carte
- Xnoy Université de Hanoi Vietnam Theorie et tolerance
- Zverev et Ghannem (MGU) Moscou mapping
- Guershenson Université de Helsinky Finlande (Bathymetrie)
- Savinych (MGU) Recteur de l’ Université (MGU) Glonass System
- Charov and Joanneum (Autriche) Reseaux Geodesique
- Klechenskaya Université de St. Petersburg (Modelisation)
- Kniazeva and koslova Mapping Aspect Russie
- Naoumov Methode de Modelisation (MGU Moscou)
- Velder Olga (Drezden University Germany) Système de Projection
- Bagrov University de Sofia (Bulgarie) Calage de Carte
- Shan Han South Korea Modelisation et compensation
- Simonian Armenian University cartography and geodesy
- Kutcher Kiev Ukraine Cartography and Bathymetry

(1)
= 0 (3)
(t1+ T) on peut se convaincre que les coordonnées (X, Y) de la position exacte du bateau et l'erreur d'horloge T font partie de l'ensemble des solutions de l'´equation
(t2+ T)
(t3+ T)
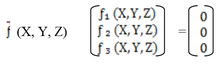
(X0, Y0, T0)
=
(6)

= −
(X0, Y0, T0). (8)
= - JT
. (9)



